what is dimensionality reduction?

Today, I am going to talk about Feature Engineer, and more specifically, PCA which is one technique in feature extraction.

Feature Engineer is an important part of machine learning. Like a quote showed above, how your algorithm does, highly depends on your data. Feature engineer include feature selection and feature extraction. We are only going to focus on feature extraction—PCA here.

What is PCA and why we are doing it?💭#

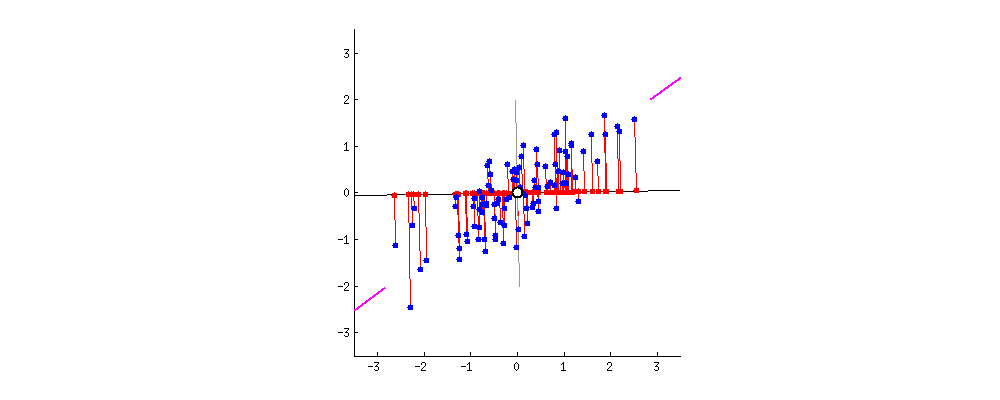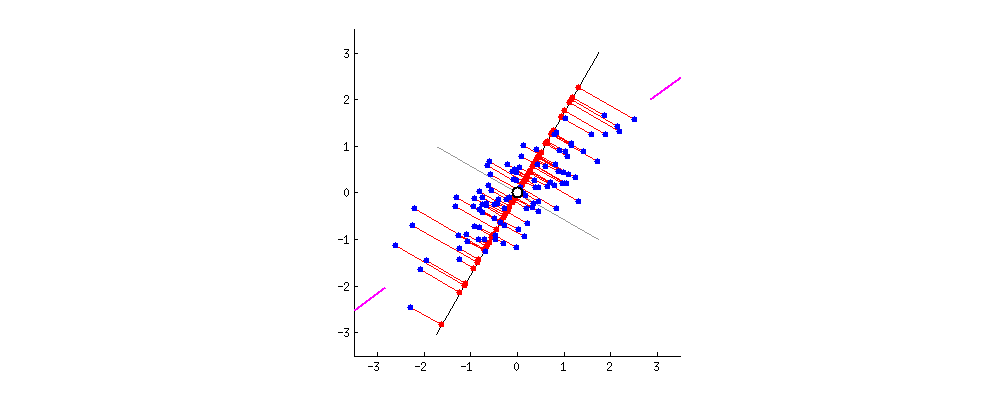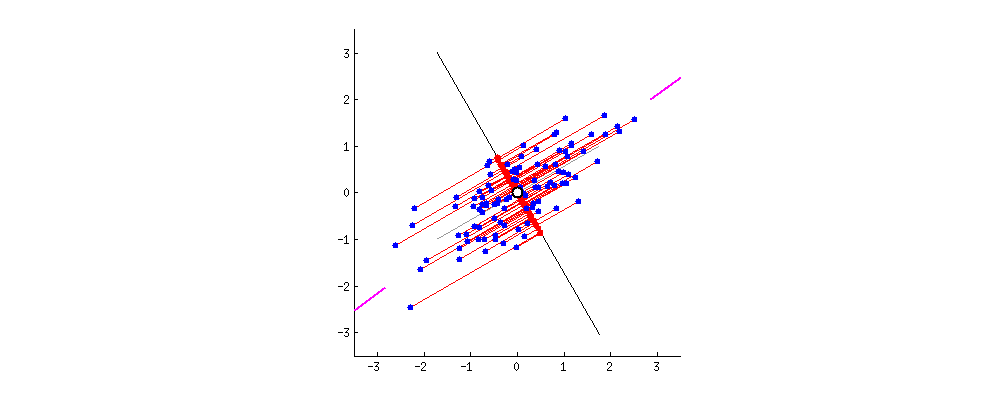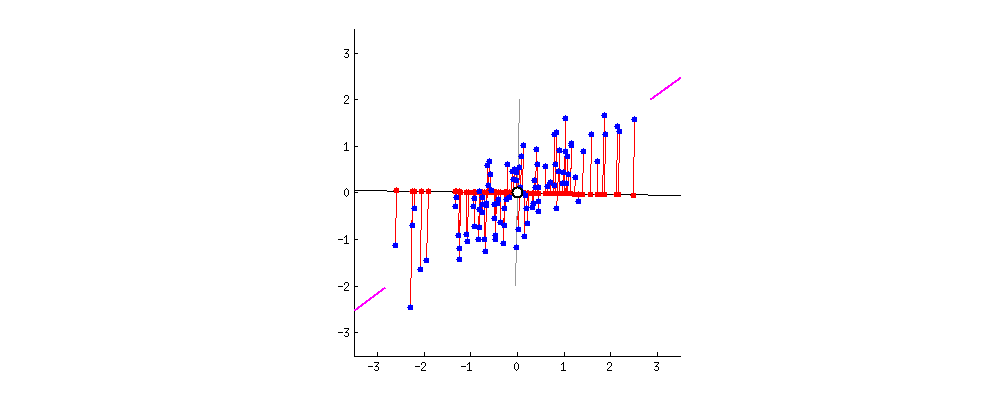
PCA refers to Principal Component Analysis. It is a way of reducing dimensions used in machine learning. What PCA actually does is finding the direction in which the data has maximum variance (because you want to capture all data points and information!). Like the picture showed below, the largest variance is with the purple line.

Feature Selection — Backward Elimination Example with code📘#

For this point, I already understood the concept “Feature Selection”, in which it calculates the P-value and get rid of the features that are unimportant. I also included this in my Machine Learning project, and I’ve attached my code below.

X_with_ones= np.append (arr=np.ones([X.shape[0],1]).astype(int), values = X, axis = 1) 
print("before Elimination, there are",X_with_ones.shape[1],"columns")

[output] before Elimination, there are 16 columns

import statsmodels.api as sm 
def backwardElimination(x, sl):
	numVars= len(x[0])
	for i in range(0, numVars):
		obj_OLS= sm.OLS(y, x).fit()
		maxVar= max(obj_OLS.pvalues).astype(float) 
		if maxVar> sl:
		    for j in range(0, numVars-i):
			    if (obj_OLS.pvalues[j].astype(float) == maxVar):
	x = np.delete(x, j, 1) obj_OLS.summary()
	return x

SL=0.05
X_modeled=backwardElimination(X_with_ones, SL)
X_modeled.shape

[output] (4240,7)

As shown above, the features are reduced to 7 from 16 after the feature selection. As we can see, there are 9 features were deleted after Backward Elimination. What’s problem with this? Because the 9 features were deleted, we missed out all the contribution that those features could bring.

Feature Extraction - PCA solves this problem!✅#

In PCA, we don’t get rid of the features. Instead, it adds new features that combine the result of other features. In this way, it retain as much information as possible. This is the main difference between PCA and feature selection.

How does PCA work 🤔#

1️⃣ We standardize the data first, because it is a very important step doing PCA. If the data is not standardized, the data with large range(0-100) will dominate the data with small range (0-1). It can be achieved by using the StandardScaler in sklearn. After standardization is done, data will be transformed into same scale.

2️⃣ After Standardization, we need to compute covariance. Remember, covariance is calculated as Cov(X,Y) = Σ E((X-μ)E(Y-ν))/n-1

Variance represents how wide the data spreads. So what does covariance mean?

It means how changes in one variable are associated with the changes in the other variable. We will calculate all the variance between each variable, and store in a matrix as showed below:

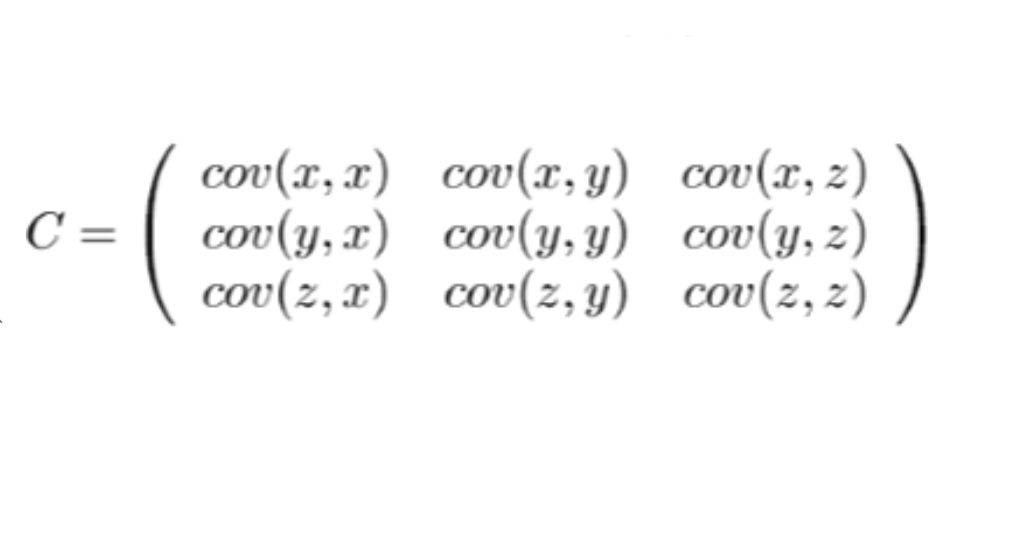
As we can see, the covariance of a variable to itself(cov(x,x), cov(y,y), cov(z,z)) is at the diagonal of this graph. Also, the matrix is symmetric. After we have the matrix, we will be able to calculate the eigenvector and eigenvalues.

The eigenvectors of the covariance matrix represent the principal components. Higher the eigenvalue, higher the variance that is captured by the corresponding vector. Therefore let’s talk about what is eigenvectors and eigenvalues, because they are the core of PCA!

3️⃣ Eigenvectors represent the directions of the principal components. We can use the following equation to solve eigenvalue:

Covariance matrix * Eigenvector = Eigenvalue * eigenvector.

Big eigenvalues correlate with important directions. As showed in picture below, we will choose to discard the smaller eigenvalue (0.04).

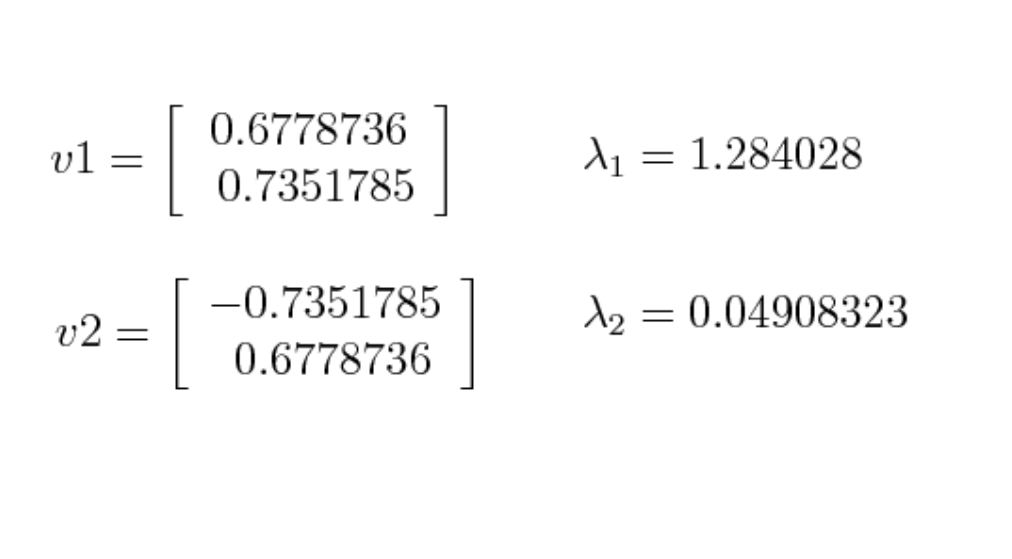
4️⃣ And we can move to the next step, which is feature vector. In this step, we will choose whether to keep or not keep those low eigenvalues, and form a vector with the remaining ones. We call this feature vector. So if we choose to keep 9 eigenvectors out of 10, our final data will contain 9 dimensions.

PCA is implemented in scikit-learn. n_components is a parameter, in which you can specify a value to decide the percentage of variance that you want to retain. For example, “PCA(n_components=0.99)” means 99% of the variance of the original features has been retained. Since in pca, our purpose is to choose the principal component, you should not use n_components=1.

5️⃣ For this last step, we need to generate our final data set because we haven’t made any change yet. We will do this by multiplying the transpose of the feature vector we got from the previous step, with the transpose of the standardized dataset.

Conclusion:🎉#

To conclude, what PCA does is to get the direction of the data with largest variance. It allows us to get rid of the smallest eigenvector that is unimportant.