what is k-fold cross validation?

In machine learning, we usually split the data into training and testing sets so that we can evaluate the model(s). This method, however, is not reliable because the accuracy of your model is largely depend on what you got! Accuracy obtained from one test set can be very different than another test set. This post will talk about K-fold Cross Validation.

The Validation Set Approach:❓#

Usually before we train a model, we spilt the data into training and test set. For example, use 80% of the data to train a model, and use 20% of the data to test our model. This approach is called The Validation Set Approach.

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test=train_test_split(X, y, test_size=0.25)

As the code shows above, we imported the train_test_split from the sklearn_model_selection package, and split the X and y dataset to train and test data, with 25% being test set and 75% being training set. However, let’s talk about why this is not the best approach.

“What is K-fold?”🤔#

“Why should I use K-fold?”🤔#

“What’s the difference between train_test_split and K-fold?”🤔#

Problems with split:

1. The final model largely depends on the train and test set you split. What does this mean?

This means the mean squared error(MSE) is largely depends on what training set and test set you get when spiltting the dataset. Therefore, the result could be very different.

2. When we have very small number of data, the result is going to be worse.

As we all know, if we have more training data, our result is usually going to be better. However, if we only have 100 rows of data, and split to 80 and 20, we only get 20 rows in test set, which is not enough. In this situation, we would get any performance due to chance.

K-fold solves the problem!✅#

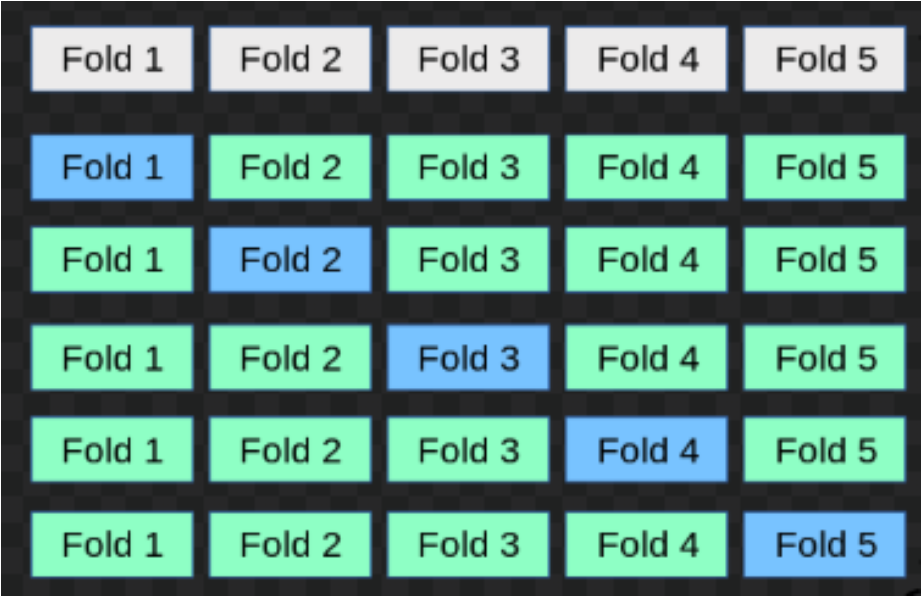
K-fold cross validation means splitting the data into k parts called “folds”. The model is then trained using k-1 folds – combined into one training set – and then the last fold is used as a test set. After repeating this process k times, we averaged to produce the overall measurement. (reference: Machine Learning with Python Cookbook).

In my machine learning project(coronary heart disease prediction), I used both train-test split and k-fold. Let’s see the code of k-fold for one of my models(logistic regression):

def run_kfold(logreg):
	kf = KFold(n_splits=10)
	outcomes = []
	fold = 0
	for train_index, test_index in kf.split(X_modeled):
		fold += 1
		X_train, X_test = X_modeled[train_index], X_modeled[test_index] 
		y_train, y_test = y[train_index], y[test_index] 
		logreg.fit(X_train, y_train)
		accuracy_lr = logreg.score(X_test, y_test)*100 outcomes.append(accuracy_lr)
		print("Fold {0} accuracy: {1}".format(fold, accuracy_lr))
	mean_outcome_logistic_regression = np.mean(outcomes)
	print("Mean Accuracy: {0}".format(mean_outcome_logistic_regression)) 
	return(mean_outcome_logistic_regression)
logreg_Kfoldscore=run_kfold(logreg)

Output:
Fold 1 accuracy: 81.36792452830188
Fold 2 accuracy: 85.84905660377359
Fold 3 accuracy: 85.84905660377359
Fold 4 accuracy: 87.97169811320755
Fold 5 accuracy: 85.84905660377359
Fold 6 accuracy: 83.9622641509434
Fold 7 accuracy: 86.55660377358491
Fold 8 accuracy: 86.08490566037736
Fold 9 accuracy: 86.08490566037736
Fold 10 accuracy: 83.9622641509434
Mean Accuracy: 85.35377358490565

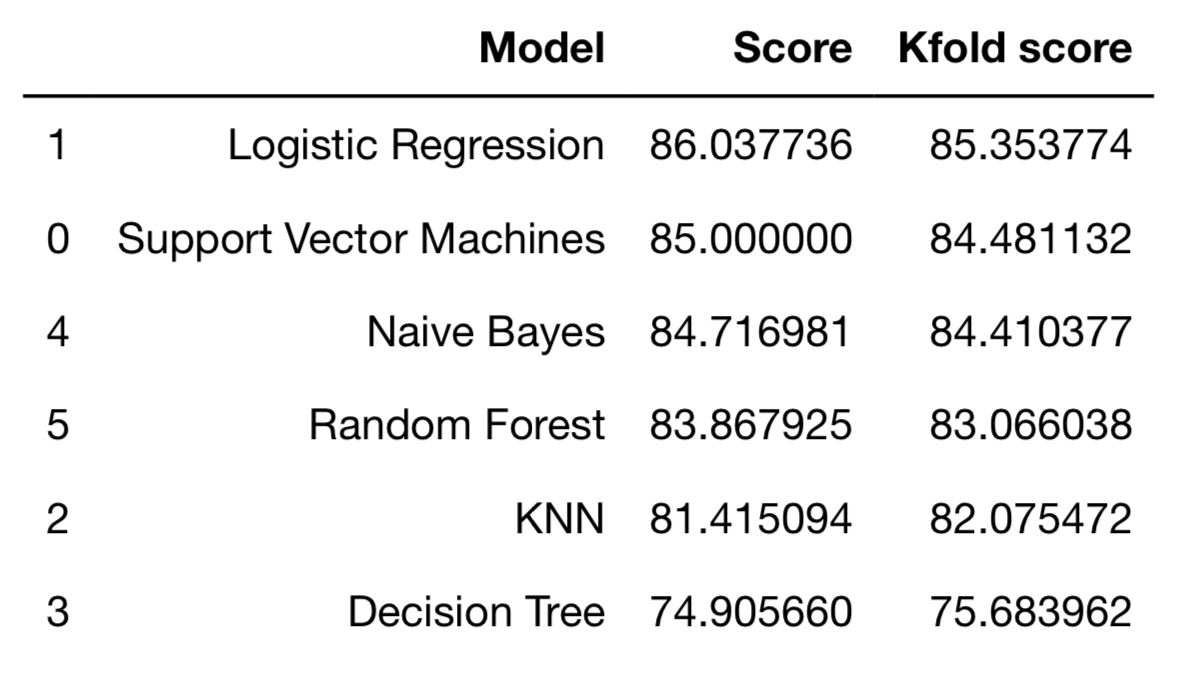
From the above code, you can see that I wrote run_kfold method to get the each accuracy among 10 interaction and calculate mean accuracy of my logistic regreesion model. I also compared the results at the end in a dataframe.

models = pd.DataFrame({
'Model': ['Support Vector Machines', 
	   'Logistic Regression',
	   'KNN',
           'Decision Tree',
	   'Naive Bayes', 
	   'Random Forest'],
    'Score': [SVM_score, Logistic_regression_score,knn_score, decision_tree_score, NB_score,
              RandomForest_score],
    'Kfold score': [svc_KFoldScore,logreg_Kfoldscore,knn_Kfoldscore,DT_Kfoldscore, nb_Kfoldscore, rf_Kfoldscore]}) 
models.sort_values(by='Score', ascending=False)